Lab: Xarray with Sea Surface Temperature (SST) data#
Here we will work with NOAA’s SST dataset, which can be accessed via:
Start by importing Numpy, Matplotlib, and Xarray. Set the default figure size to (12, 6).
1) Opening data and examining the metadata#
1.1) Open the dataset and display its contents#
1.2) Print out the long_name attribute of each variable and coordinate#
2) Basic reductions, arithmetic, means, and plotting#
2.1) Calculate the time-mean of the entire dataset#
2.2) Plot a map of the time-mean that was generated in the above part#
2.3) Calculate a spatial mean for each time, and plot this as a timeseries#
2.4) Create a weight array proportional to \(\cos(\lambda)\)#
Think carefully a about radians vs. degrees
The goal here is to realize that the dataset is provided on a \(2^o\)X\(2^o\) lat-lon grid. But we know that the distance between longitude lines shrinks as we approach the poles.
This means that if we take a naive mean (as done in the above part), we are overemphasizing the influence of the regions away from the equator (since their area is smaller but they contribute the same to the mean). So here we plan to appropriately weight our data.
2.5) Redo the calculation of the spatial mean for each time, and plot this as a timeseries#
3) Selecting and Merging Data#
For the next problem, use the following approximate locations of four different locations in the ocean.
city |
lon |
lat |
|---|---|---|
Equatorial Pacific (EP) |
250 E |
0 N |
Southern Ocean (SO) |
50 E |
60 S |
North Atlantic (NAtl) |
300 E |
30 N |
Arabian Sea (AS) |
60 E |
20 N |
3.1) Create a dataset for each point from the global dataset#
3.2) Combine these four datasets into a new dataset with the new dimension location#
Create a new dimension coordinate to hold the location name. Display the combined dataset.
3.3) Plot the SST at each location as a timeseries over the last 3 years#
4) Group by and ENSO: Reproduce the SST curve from the figure below#
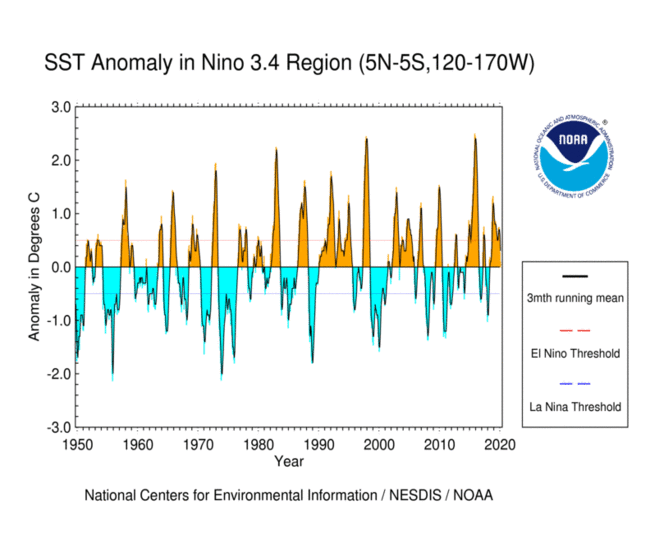
You don’t have to match the stylistic details, or use different colors above and below zero, just the “3mth running mean” curve.
Here will will calculate the NINO 3.4 index of El Nino variabillity (which is the quantity shown in the above plot) and use it to analyze datasets.
The Niño 3.4 region is defined as the region between +/- 5 deg. lat, 170 W - 120 W lon.
Warm or cold phases of the Oceanic Niño Index are defined by a five consecutive 3-month running mean of sea surface temperature (SST) anomalies in the Niño 3.4 region that is above the threshold of +0.5°C (warm), or below the threshold of -0.5°C (cold). This is known as the Oceanic Niño Index (ONI).
(Note that “anomaly” means that the seasonal cycle, also called the “climatology” has been removed.)
Also for this part: Drop the time_bnds variable as we did in class and trim the data to 1950 onward for this assignment.
