Xarray Advanced

Xarray Advanced#

– Interpolation, Groupby, Resample, Rolling, and Coarsen

In this lesson, we cover some more advanced aspects of xarray.

import numpy as np
import xarray as xr
from matplotlib import pyplot as plt
%xmode Minimal

Exception reporting mode: Minimal

Interpolation#

In the previous lesson on Xarray, we learned how to select data based on its dimension coordinates and align data with dimension different coordinates. But what if we want to estimate the value of the data variables at different coordinates. This is where interpolation comes in.

# we write it out explicitly so we can see each point.
x_data = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
f = xr.DataArray(x_data**2, dims=['x'], coords={'x': x_data})
f

<xarray.DataArray (x: 11)> Size: 88B
array([  0,   1,   4,   9,  16,  25,  36,  49,  64,  81, 100])
Coordinates:
  * x        (x) int64 88B 0 1 2 3 4 5 6 7 8 9 10
f.plot(marker='o')

[<matplotlib.lines.Line2D at 0x79647d95f440>]
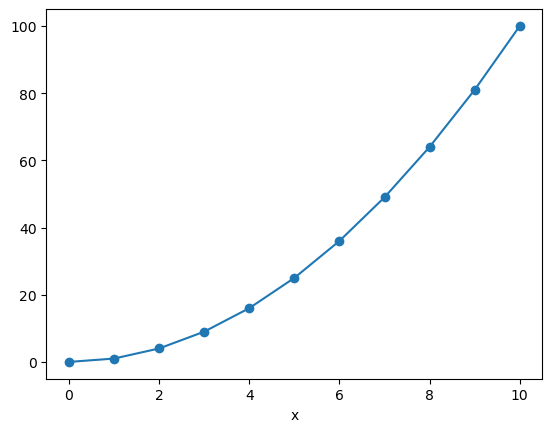
../../_images/7a4380a8758f02bd35d9e3aef88aae7e9449550e438f08298fa380ddf6045ba3.png 
f.sel(x=4)

<xarray.DataArray ()> Size: 8B
array(16)
Coordinates:
    x        int64 8B 4

We only have data on the integer points in x. But what if we wanted to estimate the value at, say, 4.5?

f.sel(x=4.5)

KeyError: 4.5


The above exception was the direct cause of the following exception:

KeyError: 4.5


The above exception was the direct cause of the following exception:

KeyError: "not all values found in index 'x'. Try setting the `method` keyword argument (example: method='nearest')."

Interpolation to the rescue!

f.sel(x=4), f.sel(x=5)

(<xarray.DataArray ()> Size: 8B
 array(16)
 Coordinates:
     x        int64 8B 4,
 <xarray.DataArray ()> Size: 8B
 array(25)
 Coordinates:
     x        int64 8B 5)

f.interp(x=4.5)

<xarray.DataArray ()> Size: 8B
array(20.5)
Coordinates:
    x        float64 8B 4.5

Interpolation uses scipy.interpolate under the hood. There are different modes of interpolation.

# default
f.interp(x=4.5, method='linear').values

array(20.5)

f.interp(x=4.5, method='nearest').values

array(16.)

f.interp(x=4.5, method='cubic').values

array(20.25)

We can interpolate to a whole new coordinate at once:

x_new = x_data + 0.5

f_interp_linear = f.interp(x=x_new, method='linear')
f_interp_cubic = f.interp(x=x_new, method='cubic')

f.plot(marker='o', label='original')
f_interp_linear.plot(marker='o', label='linear')
f_interp_cubic.plot(marker='o', label='cubic')
plt.legend()

<matplotlib.legend.Legend at 0x79647d98c470>
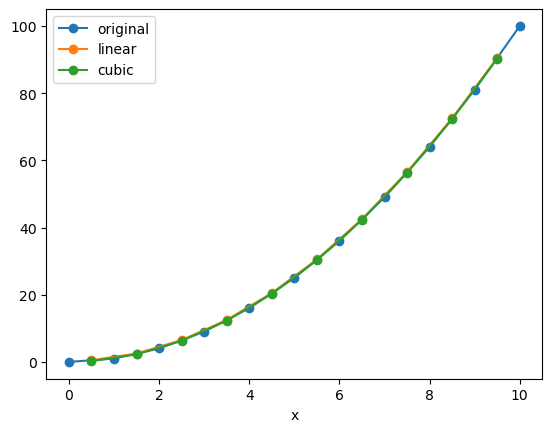
../../_images/d83a8b5134fd534c0322c60887888a9ff1dc0fd65bac764f8fb491feb87a5daa.png

Note that values outside of the original range are not supported:

f_interp_linear.values

array([ 0.5,  2.5,  6.5, 12.5, 20.5, 30.5, 42.5, 56.5, 72.5, 90.5,  nan])

Note

You can apply interpolation to any dimension, and even to multiple dimensions at a time. (Multidimensional interpolation only supports mode='nearest' and mode='linear'.) But keep in mind that Xarray has no built-in understanding of geography. If you use interp on lat / lon coordinates, it will just perform naive interpolation of the lat / lon values. More sophisticated treatment of spherical geometry requires another package such as xesmf.

Groupby#

Xarray copies Pandas’ very useful groupby functionality, enabling the “split / apply / combine” workflow on xarray DataArrays and Datasets. In the first part of the lesson, we will learn to use groupby by analyzing sea-surface temperature data.

First we load a dataset. We will use the NOAA Extended Reconstructed Sea Surface Temperature (ERSST) v5 product, a widely used and trusted gridded compilation of of historical data going back to 1854.

Since the data is provided via an OPeNDAP server, we can load it directly without downloading anything:

url = 'http://www.esrl.noaa.gov/psd/thredds/dodsC/Datasets/noaa.ersst.v5/sst.mnmean.nc'
ds = xr.open_dataset(url, drop_variables=['time_bnds'])
ds = ds.sel(time=slice('1960', '2018')).load()
ds

<xarray.Dataset> Size: 45MB
Dimensions:  (lat: 89, lon: 180, time: 708)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Data variables:
    sst      (time, lat, lon) float32 45MB -1.8 -1.8 -1.8 -1.8 ... nan nan nan
Attributes: (12/39)
    climatology:                     Climatology is based on 1971-2000 SST, X...
    description:                     In situ data: ICOADS2.5 before 2007 and ...
    keywords_vocabulary:             NASA Global Change Master Directory (GCM...
    keywords:                        Earth Science > Oceans > Ocean Temperatu...
    instrument:                      Conventional thermometers
    source_comment:                  SSTs were observed by conventional therm...
    ...                              ...
    comment:                         SSTs were observed by conventional therm...
    summary:                         ERSST.v5 is developed based on v4 after ...
    dataset_title:                   NOAA Extended Reconstructed SST V5
    _NCProperties:                   version=2,netcdf=4.6.3,hdf5=1.10.5
    data_modified:                   2025-06-03
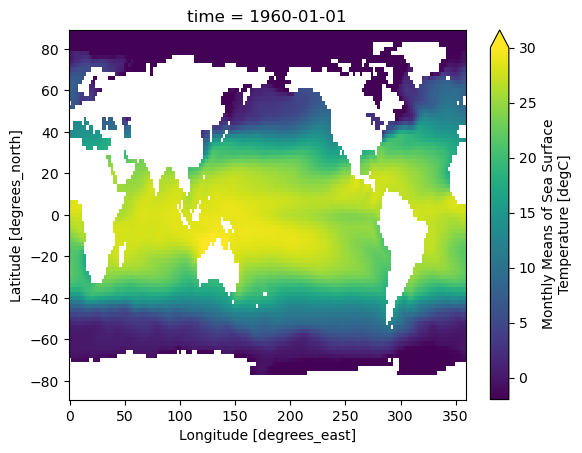
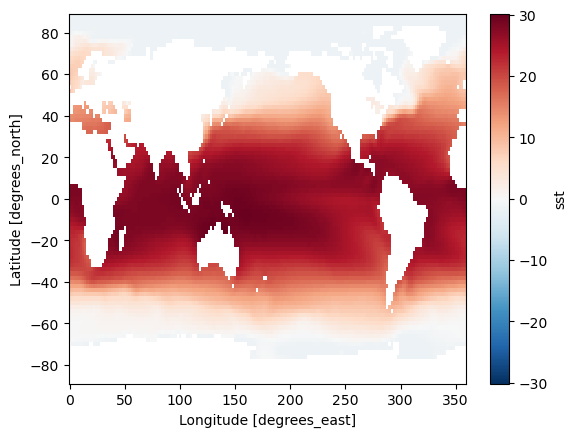
    DODS_EXTRA.Unlimited_Dimension:  time

Let’s do some basic visualizations of the data, just to make sure it looks reasonable.

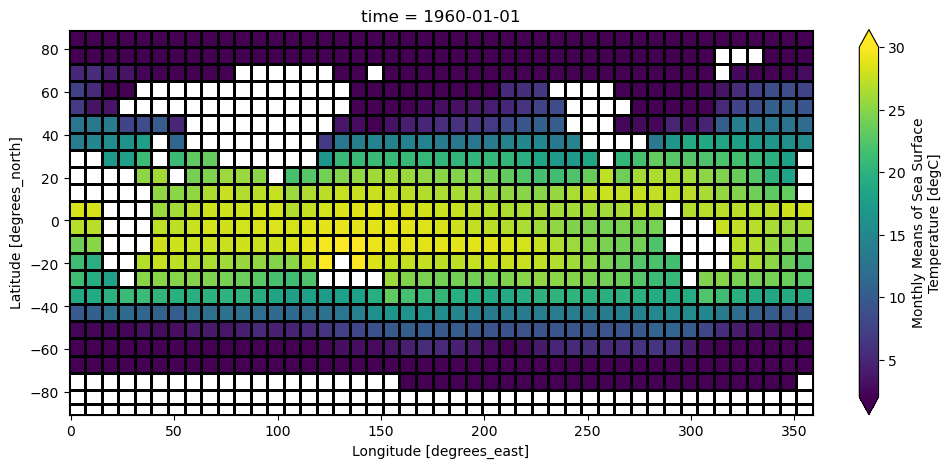
ds.sst[0].plot(vmin=-2, vmax=30)

<matplotlib.collections.QuadMesh at 0x79646c7a5250>
../../_images/cba7ae10c9419034975fc506f52bee723087936ba04676d1989c1a13a60f7ed1.png 
ds.sst.isel(time=0).plot(vmin=-2, vmax=30)

<matplotlib.collections.QuadMesh at 0x79647d9ae780>
../../_images/cba7ae10c9419034975fc506f52bee723087936ba04676d1989c1a13a60f7ed1.png

Note that xarray correctly parsed the time index, resulting in a Pandas datetime index on the time dimension.

ds.time

<xarray.DataArray 'time' (time: 708)> Size: 6kB
array(['1960-01-01T00:00:00.000000000', '1960-02-01T00:00:00.000000000',
       '1960-03-01T00:00:00.000000000', ..., '2018-10-01T00:00:00.000000000',
       '2018-11-01T00:00:00.000000000', '2018-12-01T00:00:00.000000000'],
      shape=(708,), dtype='datetime64[ns]')
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Attributes:
    long_name:        Time
    delta_t:          0000-01-00 00:00:00
    avg_period:       0000-01-00 00:00:00
    prev_avg_period:  0000-00-07 00:00:00
    standard_name:    time
    axis:             T
    actual_range:     [19723. 82300.]
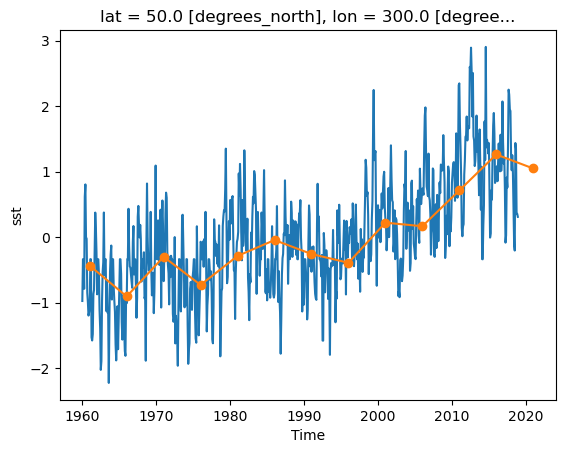
    _ChunkSizes:      1
ds.sst.sel(lon=300, lat=50).plot()

[<matplotlib.lines.Line2D at 0x796468584b00>]
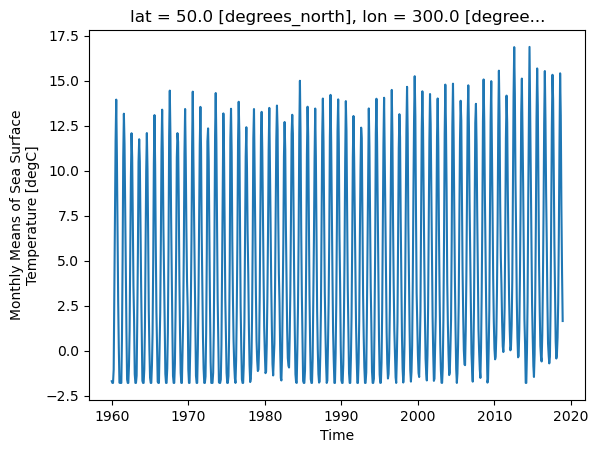
../../_images/465d172b608dd7bf02b7a484c320f728e4c486287ebf60d2ee7fdc9599d30645.png

As we can see from the plot, the timeseries at any one point is totally dominated by the seasonal cycle. We would like to remove this seasonal cycle (called the “climatology”) in order to better see the long-term variaitions in temperature. We will accomplish this using groupby.

The syntax of Xarray’s groupby is almost identical to Pandas. We will first apply groupby to a single DataArray.

ds.sst.groupby?

Split Step#

The most important argument is group: this defines the unique values we will us to “split” the data for grouped analysis. We can pass either a DataArray or a name of a variable in the dataset. Lets first use a DataArray. Just like with Pandas, we can use the time indexe to extract specific components of dates and times. Xarray uses a special syntax for this .dt, called the DatetimeAccessor.

ds.time

<xarray.DataArray 'time' (time: 708)> Size: 6kB
array(['1960-01-01T00:00:00.000000000', '1960-02-01T00:00:00.000000000',
       '1960-03-01T00:00:00.000000000', ..., '2018-10-01T00:00:00.000000000',
       '2018-11-01T00:00:00.000000000', '2018-12-01T00:00:00.000000000'],
      shape=(708,), dtype='datetime64[ns]')
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Attributes:
    long_name:        Time
    delta_t:          0000-01-00 00:00:00
    avg_period:       0000-01-00 00:00:00
    prev_avg_period:  0000-00-07 00:00:00
    standard_name:    time
    axis:             T
    actual_range:     [19723. 82300.]
    _ChunkSizes:      1
ds.time.dt.month

<xarray.DataArray 'month' (time: 708)> Size: 6kB
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,
        6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,
       11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,
        4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,
        9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,
        2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,
        7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11,
       12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,
        5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9,
       10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,
        3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,
        8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
        1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,
        6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,
       11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,
        4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,
        9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,
        2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,
        7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11,
       12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,
...
        3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,
        8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
        1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,
        6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,
       11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,
        4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,
        9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,
        2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,
        7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11,
       12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,
        5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9,
       10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,
        3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,
        8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
        1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,
        6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10,
       11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,
        4,  5,  6,  7,  8,  9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,
        9, 10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,  1,
        2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Attributes:
    long_name:        Time
    delta_t:          0000-01-00 00:00:00
    avg_period:       0000-01-00 00:00:00
    prev_avg_period:  0000-00-07 00:00:00
    standard_name:    time
    axis:             T
    actual_range:     [19723. 82300.]
    _ChunkSizes:      1
ds.time.dt.year

<xarray.DataArray 'year' (time: 708)> Size: 6kB
array([1960, 1960, 1960, 1960, 1960, 1960, 1960, 1960, 1960, 1960, 1960,
       1960, 1961, 1961, 1961, 1961, 1961, 1961, 1961, 1961, 1961, 1961,
       1961, 1961, 1962, 1962, 1962, 1962, 1962, 1962, 1962, 1962, 1962,
       1962, 1962, 1962, 1963, 1963, 1963, 1963, 1963, 1963, 1963, 1963,
       1963, 1963, 1963, 1963, 1964, 1964, 1964, 1964, 1964, 1964, 1964,
       1964, 1964, 1964, 1964, 1964, 1965, 1965, 1965, 1965, 1965, 1965,
       1965, 1965, 1965, 1965, 1965, 1965, 1966, 1966, 1966, 1966, 1966,
       1966, 1966, 1966, 1966, 1966, 1966, 1966, 1967, 1967, 1967, 1967,
       1967, 1967, 1967, 1967, 1967, 1967, 1967, 1967, 1968, 1968, 1968,
       1968, 1968, 1968, 1968, 1968, 1968, 1968, 1968, 1968, 1969, 1969,
       1969, 1969, 1969, 1969, 1969, 1969, 1969, 1969, 1969, 1969, 1970,
       1970, 1970, 1970, 1970, 1970, 1970, 1970, 1970, 1970, 1970, 1970,
       1971, 1971, 1971, 1971, 1971, 1971, 1971, 1971, 1971, 1971, 1971,
       1971, 1972, 1972, 1972, 1972, 1972, 1972, 1972, 1972, 1972, 1972,
       1972, 1972, 1973, 1973, 1973, 1973, 1973, 1973, 1973, 1973, 1973,
       1973, 1973, 1973, 1974, 1974, 1974, 1974, 1974, 1974, 1974, 1974,
       1974, 1974, 1974, 1974, 1975, 1975, 1975, 1975, 1975, 1975, 1975,
       1975, 1975, 1975, 1975, 1975, 1976, 1976, 1976, 1976, 1976, 1976,
       1976, 1976, 1976, 1976, 1976, 1976, 1977, 1977, 1977, 1977, 1977,
       1977, 1977, 1977, 1977, 1977, 1977, 1977, 1978, 1978, 1978, 1978,
...
       2001, 2001, 2001, 2001, 2001, 2001, 2001, 2001, 2001, 2002, 2002,
       2002, 2002, 2002, 2002, 2002, 2002, 2002, 2002, 2002, 2002, 2003,
       2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003, 2003,
       2004, 2004, 2004, 2004, 2004, 2004, 2004, 2004, 2004, 2004, 2004,
       2004, 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005,
       2005, 2005, 2006, 2006, 2006, 2006, 2006, 2006, 2006, 2006, 2006,
       2006, 2006, 2006, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007,
       2007, 2007, 2007, 2007, 2008, 2008, 2008, 2008, 2008, 2008, 2008,
       2008, 2008, 2008, 2008, 2008, 2009, 2009, 2009, 2009, 2009, 2009,
       2009, 2009, 2009, 2009, 2009, 2009, 2010, 2010, 2010, 2010, 2010,
       2010, 2010, 2010, 2010, 2010, 2010, 2010, 2011, 2011, 2011, 2011,
       2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2012, 2012, 2012,
       2012, 2012, 2012, 2012, 2012, 2012, 2012, 2012, 2012, 2013, 2013,
       2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2014,
       2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014,
       2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015,
       2015, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016,
       2016, 2016, 2017, 2017, 2017, 2017, 2017, 2017, 2017, 2017, 2017,
       2017, 2017, 2017, 2018, 2018, 2018, 2018, 2018, 2018, 2018, 2018,
       2018, 2018, 2018, 2018])
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Attributes:
    long_name:        Time
    delta_t:          0000-01-00 00:00:00
    avg_period:       0000-01-00 00:00:00
    prev_avg_period:  0000-00-07 00:00:00
    standard_name:    time
    axis:             T
    actual_range:     [19723. 82300.]
    _ChunkSizes:      1

We can use these arrays in a groupby operation:

gb = ds.sst.groupby(ds.time.dt.month)
gb

<DataArrayGroupBy, grouped over 1 grouper(s), 12 groups in total:
    'month': 12/12 groups present with labels 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12>

Xarray also offers a more concise syntax when the variable you’re grouping on is already present in the dataset. This is identical to the previous line:

gb = ds.sst.groupby('time.month')
gb

<DataArrayGroupBy, grouped over 1 grouper(s), 12 groups in total:
    'month': 12/12 groups present with labels 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12>

Now that the data are split, we can manually iterate over the group. The iterator returns the key (group name) and the value (the actual dataset corresponding to that group) for each group.

for group_name, group_da in gb:
    # stop iterating after the first loop
    break 
print(group_name)
group_da

1

<xarray.DataArray 'sst' (time: 59, lat: 89, lon: 180)> Size: 4MB
array([[[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        ...,
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan]],

       [[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        ...,
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan]],

       [[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        ...,
...
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan]],

       [[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        ...,
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan]],

       [[-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        [-1.8, -1.8, -1.8, ..., -1.8, -1.8, -1.8],
        ...,
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan],
        [ nan,  nan,  nan, ...,  nan,  nan,  nan]]],
      shape=(59, 89, 180), dtype=float32)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * time     (time) datetime64[ns] 472B 1960-01-01 1961-01-01 ... 2018-01-01
Attributes:
    long_name:     Monthly Means of Sea Surface Temperature
    units:         degC
    var_desc:      Sea Surface Temperature
    level_desc:    Surface
    statistic:     Mean
    dataset:       NOAA Extended Reconstructed SST V5
    parent_stat:   Individual Values
    actual_range:  [-1.8     42.32636]
    valid_range:   [-1.8 45. ]
    _ChunkSizes:   [  1  89 180]
group_da.mean('time').plot()

<matplotlib.collections.QuadMesh at 0x79646298fe00>
../../_images/346b9751169533d78b46381482c906c4a883f3baba11afa34886107b0cd2eb03.png

Map & Combine#

Now that we have groups defined, it’s time to “apply” a calculation to the group. Like in Pandas, these calculations can either be:

  • aggregation: reduces the size of the group

  • transformation: preserves the group’s full size

At then end of the apply step, xarray will automatically combine the aggregated / transformed groups back into a single object.

Warning

Xarray calls the “apply” step map. This is different from Pandas!

The most fundamental way to apply is with the .map method.

gb.map?

Aggregations#

.map accepts as its argument a function. We can pass an existing function:

gb.map(np.mean)

<xarray.DataArray 'sst' (month: 12)> Size: 48B
array([13.659799, 13.768786, 13.765035, 13.684187, 13.642321, 13.712923,
       13.92192 , 14.094068, 13.982326, 13.691306, 13.506638, 13.529599],
      dtype=float32)
Coordinates:
  * month    (month) int64 96B 1 2 3 4 5 6 7 8 9 10 11 12

Because we specified no extra arguments (like axis) the function was applied over all space and time dimensions. This is not what we wanted. Instead, we could define a custom function. This function takes a single argument–the group dataset–and returns a new dataset to be combined:

def time_mean(a):
    return a.mean(dim='time')

gb.map(time_mean)

<xarray.DataArray 'sst' (month: 12, lat: 89, lon: 180)> Size: 769kB
array([[[-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        [-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        [-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        ...,
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]],

       [[-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        [-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        [-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
...
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]],

       [[-1.7995418, -1.7996342, -1.7998586, ..., -1.7997911,
         -1.7996678, -1.7995375],
        [-1.7995987, -1.7997787, -1.8      , ..., -1.8      ,
         -1.7998224, -1.7996234],
        [-1.8      , -1.8      , -1.8      , ..., -1.8      ,
         -1.8      , -1.8      ],
        ...,
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]]], shape=(12, 89, 180), dtype=float32)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
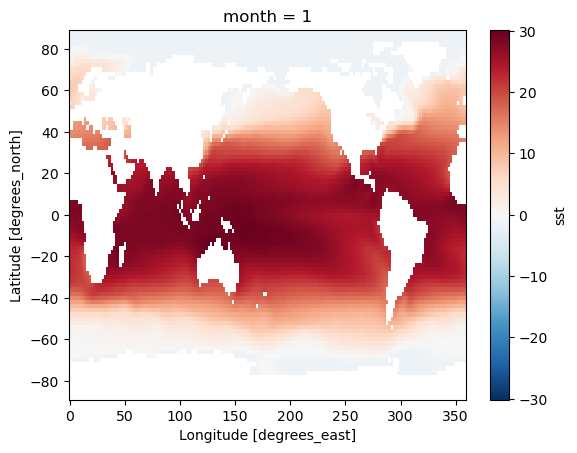
  * month    (month) int64 96B 1 2 3 4 5 6 7 8 9 10 11 12
gb.map(time_mean).sel(month=1).plot()

<matplotlib.collections.QuadMesh at 0x796462984ce0>
../../_images/b495e7ccabab9e2af338dff230b536c72f19df01500e2110fa8dc7dd3274415b.png

Like Pandas, xarray’s groupby object has many built-in aggregation operations (e.g. mean, min, max, std, etc):

# this does the same thing as the previous cell
sst_mm = gb.mean('time')
sst_mm

<xarray.DataArray 'sst' (month: 12, lat: 89, lon: 180)> Size: 769kB
array([[[-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        [-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        [-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        ...,
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]],

       [[-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        [-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        [-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
...
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]],

       [[-1.7995427, -1.799635 , -1.7998594, ..., -1.7997919,
         -1.7996687, -1.7995385],
        [-1.7995995, -1.7997797, -1.8000009, ..., -1.8000009,
         -1.7998233, -1.7996242],
        [-1.8000009, -1.8000009, -1.8000009, ..., -1.8000009,
         -1.8000009, -1.8000009],
        ...,
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]]], shape=(12, 89, 180), dtype=float32)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * month    (month) int64 96B 1 2 3 4 5 6 7 8 9 10 11 12
Attributes:
    long_name:     Monthly Means of Sea Surface Temperature
    units:         degC
    var_desc:      Sea Surface Temperature
    level_desc:    Surface
    statistic:     Mean
    dataset:       NOAA Extended Reconstructed SST V5
    parent_stat:   Individual Values
    actual_range:  [-1.8     42.32636]
    valid_range:   [-1.8 45. ]
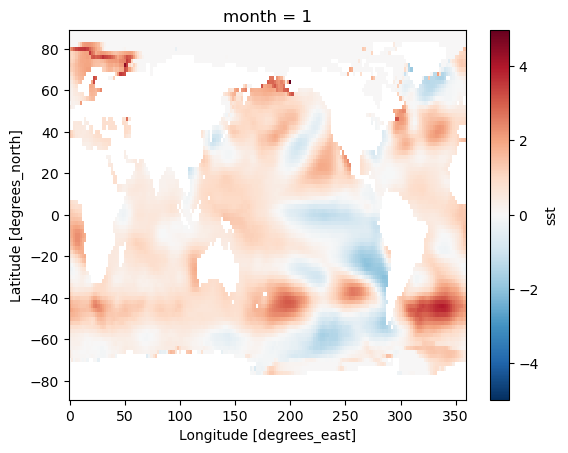
    _ChunkSizes:   [  1  89 180]

So we did what we wanted to do: calculate the climatology at every point in the dataset. Let’s look at the data a bit.

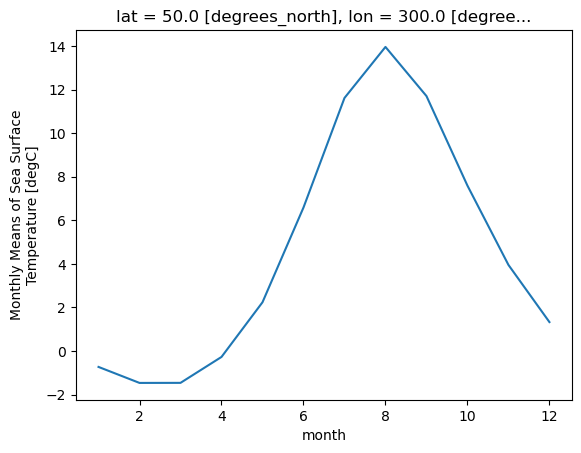
Climatlogy at a specific point in the North Atlantic

sst_mm.sel(lon=300, lat=50).plot()

[<matplotlib.lines.Line2D at 0x79645e1c4590>]
../../_images/8dee8ee85d0f5156322b25382b3f60df88a68e762a0dd6ac68636108ff36fdf1.png

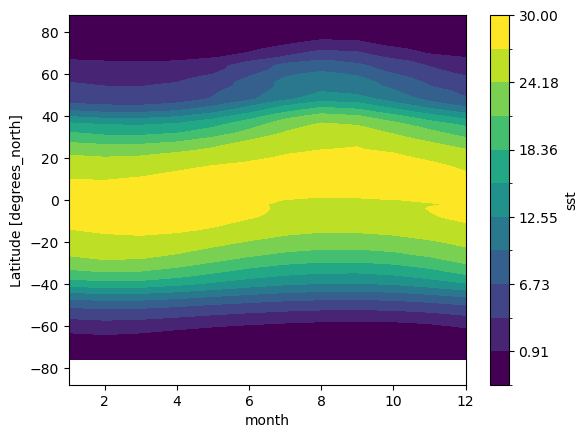
Zonal Mean Climatolgoy

sst_mm.mean(dim='lon').transpose().plot.contourf(levels=12, vmin=-2, vmax=30)

<matplotlib.contour.QuadContourSet at 0x79645e239910>
../../_images/3e60aca703172c1f0112418a9e471196dcac34cf04081e006477b95512173f47.png

Difference between January and July Climatology

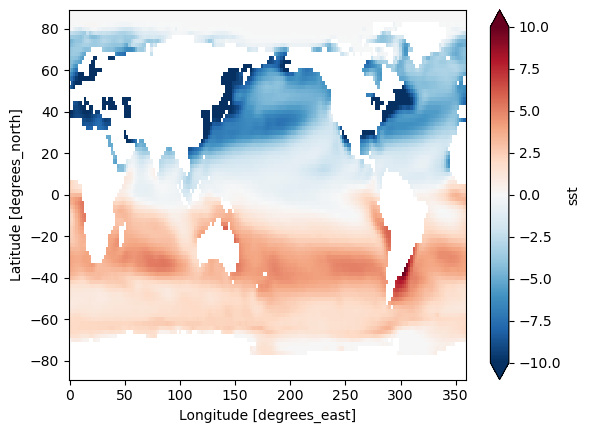
(sst_mm.sel(month=1) - sst_mm.sel(month=7)).plot(vmax=10)

<matplotlib.collections.QuadMesh at 0x79645e32e2a0>
../../_images/0a146bfacfa58d720ba58178ab05874819a1dc39acf978f962429e7cb853deae.png

Transformations#

Now we want to remove this climatology from the dataset, to examine the residual, called the anomaly, which is the interesting part from a climate perspective. Removing the seasonal climatology is a perfect example of a transformation: it operates over a group, but doesn’t change the size of the dataset. Here is one way to code it.

def remove_time_mean(x):
    return x - x.mean(dim='time')

ds_anom = ds.groupby('time.month').map(remove_time_mean)
ds_anom

<xarray.Dataset> Size: 45MB
Dimensions:  (time: 708, lat: 89, lon: 180)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
Data variables:
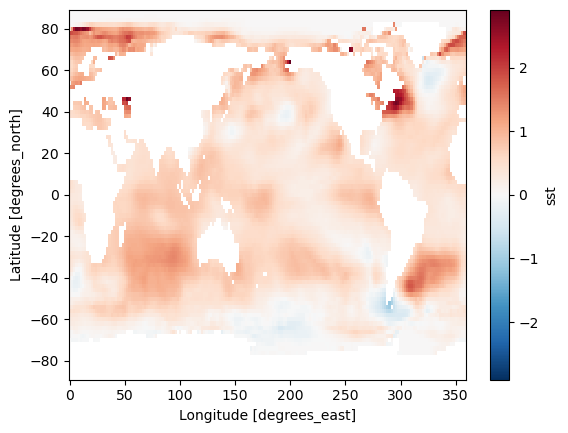
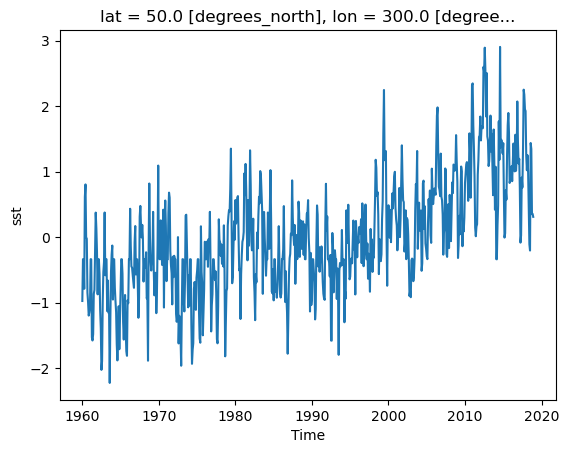
    sst      (time, lat, lon) float32 45MB 0.0 0.0 0.0 0.0 ... nan nan nan nan
ds_anom.sst.sel(lon=300, lat=50).plot()

[<matplotlib.lines.Line2D at 0x79645e1a6720>]
../../_images/20720bb9d0cae5b013f4072c28da4a2af755240728e35d4259ea698efa1779af.png

Note

In the above example, we applied groupby to a Dataset instead of a DataArray.

Xarray makes these sorts of transformations easy by supporting groupby arithmetic. This concept is easiest explained with an example:

gb = ds.groupby('time.month')
ds_anom = gb - gb.mean(dim='time')
ds_anom

<xarray.Dataset> Size: 45MB
Dimensions:  (lat: 89, lon: 180, time: 708)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
    month    (time) int64 6kB 1 2 3 4 5 6 7 8 9 10 11 ... 3 4 5 6 7 8 9 10 11 12
Data variables:
    sst      (time, lat, lon) float32 45MB 9.537e-07 9.537e-07 ... nan nan

Now we can view the climate signal without the overwhelming influence of the seasonal cycle.

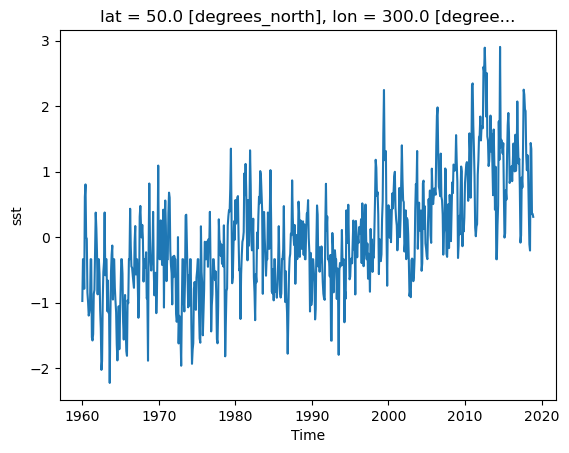
Timeseries at a single point in the North Atlantic

ds_anom.sst.sel(lon=300, lat=50).plot()

[<matplotlib.lines.Line2D at 0x79645df4bd40>]
../../_images/eb583d8afc53df184212729bfaf6647405a13259cda7760c4a8a9933337fdfce.png

Difference between Jan. 1 2018 and Jan. 1 1960

(ds_anom.sel(time='2018-01-01') - ds_anom.sel(time='1960-01-01')).sst.plot()

<matplotlib.collections.QuadMesh at 0x79645e029ca0>
../../_images/605a9bd4e5d0566a899722cb493cd3b125e3b1af6a508b42e15d93a095ae5371.png

Coarsen#

coarsen is a simple way to reduce the size of your data along one or more axes. It is very similar to resample when operating on time dimensions; the key difference is that coarsen only operates on fixed blocks of data, irrespective of the coordinate values, while resample actually looks at the coordinates to figure out, e.g. what month a particular data point is in.

For regularly-spaced monthly data beginning in January, the following should be equivalent to annual resampling. However, results would different for irregularly-spaced data.

ds.coarsen(time=12).mean()

<xarray.Dataset> Size: 4MB
Dimensions:  (time: 59, lat: 89, lon: 180)
Coordinates:
  * lat      (lat) float32 356B 88.0 86.0 84.0 82.0 ... -82.0 -84.0 -86.0 -88.0
  * lon      (lon) float32 720B 0.0 2.0 4.0 6.0 8.0 ... 352.0 354.0 356.0 358.0
  * time     (time) datetime64[ns] 472B 1960-06-16T08:00:00 ... 2018-06-16T12...
Data variables:
    sst      (time, lat, lon) float32 4MB -1.8 -1.8 -1.8 -1.8 ... nan nan nan
Attributes: (12/39)
    climatology:                     Climatology is based on 1971-2000 SST, X...
    description:                     In situ data: ICOADS2.5 before 2007 and ...
    keywords_vocabulary:             NASA Global Change Master Directory (GCM...
    keywords:                        Earth Science > Oceans > Ocean Temperatu...
    instrument:                      Conventional thermometers
    source_comment:                  SSTs were observed by conventional therm...
    ...                              ...
    comment:                         SSTs were observed by conventional therm...
    summary:                         ERSST.v5 is developed based on v4 after ...
    dataset_title:                   NOAA Extended Reconstructed SST V5
    _NCProperties:                   version=2,netcdf=4.6.3,hdf5=1.10.5
    data_modified:                   2025-06-03
    DODS_EXTRA.Unlimited_Dimension:  time

Coarsen also works on spatial coordinates (or any coordiantes).

ds_coarse = ds.coarsen(lon=4, lat=4, boundary='pad').mean()
ds_coarse.sst.isel(time=0).plot(vmin=2, vmax=30, figsize=(12, 5), edgecolor='k')

<matplotlib.collections.QuadMesh at 0x7964598ee9f0>
../../_images/78adc950b9e06027a702ab04971f4a1769da3924ee6ac2c2075d389d882d563c.png

An Advanced Example#

In this example we will show a realistic workflow with Xarray. We will

  • Load a “basin mask” dataset

  • Interpolate the basins to our SST dataset coordinates

  • Group the SST by basin

  • Convert to Pandas Dataframe and plot mean SST by basin

basin = xr.open_dataset('http://iridl.ldeo.columbia.edu/SOURCES/.NOAA/.NODC/.WOA09/.Masks/.basin/dods')
basin

<xarray.Dataset> Size: 9MB
Dimensions:  (X: 360, Y: 180, Z: 33)
Coordinates:
  * X        (X) float32 1kB 0.5 1.5 2.5 3.5 4.5 ... 356.5 357.5 358.5 359.5
  * Y        (Y) float32 720B -89.5 -88.5 -87.5 -86.5 ... 86.5 87.5 88.5 89.5
  * Z        (Z) float32 132B 0.0 10.0 20.0 30.0 ... 4e+03 4.5e+03 5e+03 5.5e+03
Data variables:
    basin    (Z, Y, X) float32 9MB ...
Attributes:
    Conventions:  IRIDL
basin = basin.rename({'X': 'lon', 'Y': 'lat'})
basin

<xarray.Dataset> Size: 9MB
Dimensions:  (lon: 360, lat: 180, Z: 33)
Coordinates:
  * lon      (lon) float32 1kB 0.5 1.5 2.5 3.5 4.5 ... 356.5 357.5 358.5 359.5
  * lat      (lat) float32 720B -89.5 -88.5 -87.5 -86.5 ... 86.5 87.5 88.5 89.5
  * Z        (Z) float32 132B 0.0 10.0 20.0 30.0 ... 4e+03 4.5e+03 5e+03 5.5e+03
Data variables:
    basin    (Z, lat, lon) float32 9MB ...
Attributes:
    Conventions:  IRIDL
basin_surf = basin.basin[0]
basin_surf

<xarray.DataArray 'basin' (lat: 180, lon: 360)> Size: 259kB
[64800 values with dtype=float32]
Coordinates:
  * lon      (lon) float32 1kB 0.5 1.5 2.5 3.5 4.5 ... 356.5 357.5 358.5 359.5
  * lat      (lat) float32 720B -89.5 -88.5 -87.5 -86.5 ... 86.5 87.5 88.5 89.5
    Z        float32 4B 0.0
Attributes:
    long_name:  basin code
    scale_max:  58
    CLIST:      Atlantic Ocean\nPacific Ocean \nIndian Ocean\nMediterranean S...
    valid_min:  1
    valid_max:  58
    scale_min:  1
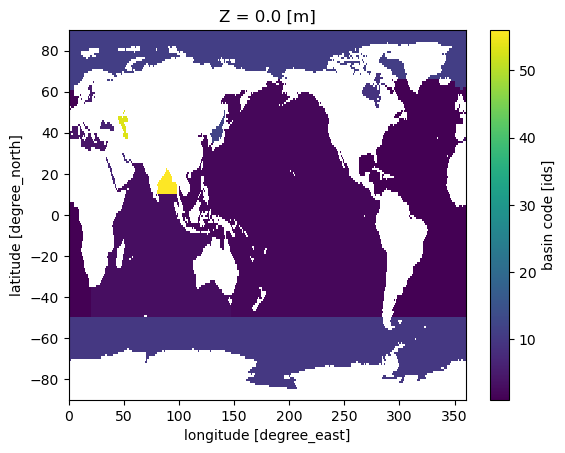
    units:      ids
basin_surf.plot()

<matplotlib.collections.QuadMesh at 0x796459db5820>
../../_images/2f860040f87a8a20178c7876d399a1d66ff5c358350ef0cbc3ad0f7325f0555f.png 
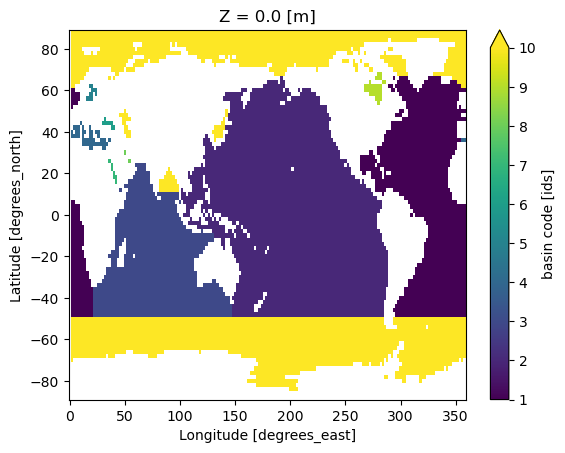
basin_surf_interp = basin_surf.interp_like(ds.sst, method='nearest')
basin_surf_interp.plot(vmax=10)

<matplotlib.collections.QuadMesh at 0x7964599c3aa0>
../../_images/b7d076b8831477903a3710d78c0697bddc9f2ac2e3430b577f75dae4a0d7d8a7.png 
ds.sst.groupby(basin_surf_interp).first()

<xarray.DataArray 'sst' (time: 708, basin: 14)> Size: 40kB
array([[-1.8       , -1.8       , 23.455315  , ..., -1.8       ,
         3.3971915 , 24.182198  ],
       [-1.8       , -1.8       , 23.722523  , ..., -1.8       ,
         0.03573781, 24.59657   ],
       [-1.8       , -1.8       , 24.601315  , ..., -1.8       ,
        -0.26487017, 26.234186  ],
       ...,
       [ 0.74060076,  6.234071  , 29.29452   , ..., 10.828896  ,
        15.948308  , 29.411022  ],
       [-0.7154853 ,  3.0145268 , 27.62134   , ...,  5.319496  ,
        10.6545925 , 27.738274  ],
       [-1.8       , -0.08144638, 25.895384  , ...,  0.43054962,
         7.241315  , 26.150328  ]], shape=(708, 14), dtype=float32)
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
    Z        float32 4B 0.0
  * basin    (basin) float32 56B 1.0 2.0 3.0 4.0 5.0 ... 11.0 12.0 53.0 56.0
Attributes:
    long_name:     Monthly Means of Sea Surface Temperature
    units:         degC
    var_desc:      Sea Surface Temperature
    level_desc:    Surface
    statistic:     Mean
    dataset:       NOAA Extended Reconstructed SST V5
    parent_stat:   Individual Values
    actual_range:  [-1.8     42.32636]
    valid_range:   [-1.8 45. ]
    _ChunkSizes:   [  1  89 180]
basin_mean_sst = ds.sst.groupby(basin_surf_interp).mean()
basin_mean_sst

<xarray.DataArray 'sst' (time: 708, basin: 14)> Size: 40kB
array([[18.585493 , 20.757555 , 21.572067 , ...,  6.238062 ,  6.889794 ,
        26.49982  ],
       [18.705065 , 20.81674  , 21.902279 , ...,  4.8877654,  5.44638  ,
        26.577093 ],
       [18.845842 , 20.865038 , 22.031416 , ...,  4.686406 ,  5.5322194,
        27.908558 ],
       ...,
       [19.851126 , 21.961922 , 20.391016 , ..., 17.577967 , 18.201479 ,
        29.344082 ],
       [19.424864 , 21.726126 , 21.063389 , ..., 13.47003  , 13.878287 ,
        28.759714 ],
       [19.265856 , 21.514656 , 21.816141 , ...,  9.421737 , 10.615019 ,
        27.90872  ]], shape=(708, 14), dtype=float32)
Coordinates:
  * time     (time) datetime64[ns] 6kB 1960-01-01 1960-02-01 ... 2018-12-01
    Z        float32 4B 0.0
  * basin    (basin) float32 56B 1.0 2.0 3.0 4.0 5.0 ... 11.0 12.0 53.0 56.0
Attributes:
    long_name:     Monthly Means of Sea Surface Temperature
    units:         degC
    var_desc:      Sea Surface Temperature
    level_desc:    Surface
    statistic:     Mean
    dataset:       NOAA Extended Reconstructed SST V5
    parent_stat:   Individual Values
    actual_range:  [-1.8     42.32636]
    valid_range:   [-1.8 45. ]
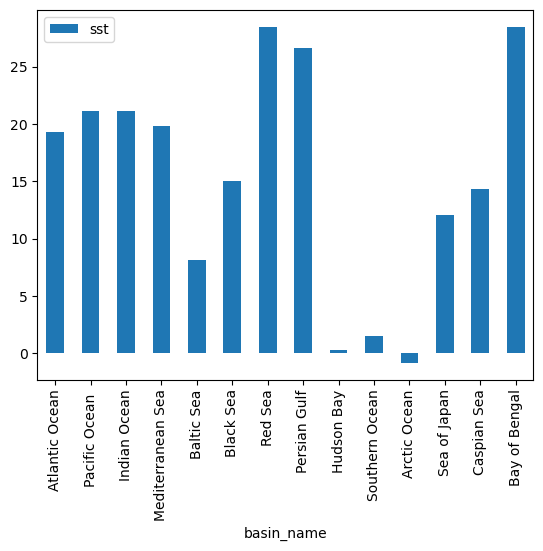
    _ChunkSizes:   [  1  89 180]
df = basin_mean_sst.mean('time').to_dataframe()
df
Z sst
basin
1.0 0.0 19.285166
2.0 0.0 21.178267
3.0 0.0 21.127174
4.0 0.0 19.845957
5.0 0.0 8.132104
6.0 0.0 15.082788
7.0 0.0 28.493765
8.0 0.0 26.618376
9.0 0.0 0.310864
10.0 0.0 1.547827
11.0 0.0 -0.816736
12.0 0.0 12.086259
53.0 0.0 14.337825
56.0 0.0 28.465954 
import pandas as pd
basin_names = basin_surf.attrs['CLIST'].split('\n')
basin_df = pd.Series(basin_names, index=np.arange(1, len(basin_names)+1))
basin_df

1                 Atlantic Ocean
2                 Pacific Ocean 
3                   Indian Ocean
4              Mediterranean Sea
5                     Baltic Sea
6                      Black Sea
7                        Red Sea
8                   Persian Gulf
9                     Hudson Bay
10                Southern Ocean
11                  Arctic Ocean
12                  Sea of Japan
13                      Kara Sea
14                      Sulu Sea
15                    Baffin Bay
16            East Mediterranean
17            West Mediterranean
18                Sea of Okhotsk
19                     Banda Sea
20                 Caribbean Sea
21                 Andaman Basin
22               North Caribbean
23                Gulf of Mexico
24                  Beaufort Sea
25               South China Sea
26                   Barents Sea
27                   Celebes Sea
28                Aleutian Basin
29                    Fiji Basin
30          North American Basin
31           West European Basin
32        Southeast Indian Basin
33                     Coral Sea
34             East Indian Basin
35          Central Indian Basin
36      Southwest Atlantic Basin
37      Southeast Atlantic Basin
38       Southeast Pacific Basin
39               Guatemala Basin
40           East Caroline Basin
41                Marianas Basin
42                Philippine Sea
43                   Arabian Sea
44                   Chile Basin
45                  Somali Basin
46               Mascarene Basin
47                  Crozet Basin
48                  Guinea Basin
49                  Brazil Basin
50               Argentine Basin
51                    Tasman Sea
52         Atlantic Indian Basin
53                   Caspian Sea
54                   Sulu Sea II
55               Venezuela Basin
56                 Bay of Bengal
57                      Java Sea
58    East Indian Atlantic Basin
dtype: object

df = df.join(basin_df.rename('basin_name'))

df.plot.bar(y='sst', x='basin_name')

<Axes: xlabel='basin_name'>
../../_images/df2c4bf41946f245f1c0ad13f8e1897ac0d1856348be2c11809ab629aab29dab.png
Contents